Analyse Structurelle des Interférences (A.S.I.)
bref aperçu sur l’«Analyse Structurelle des Interférences» (A.S.I.)
= méthode cohérente de traitement statistique des répartitions numériques complexes,
tableaux multidimensionnels.
_____________________
La première présentation de cette méthode originale se trouve dans la revue technique bien connue à l’époque, Informatique et Sciences humaines, N° 39, Paris, décembre 1978, pp. 11-96 – publiée par l’Institut des Sciences Humaines Appliquées [Université Paris-Sorbonne] avec le concours de l’U.E.R. de Mathématiques, Logique Formelle et Informatique [Université René Descartes] et du Département de Mathématiques et d’Informatique Appliquées aux Sciences Humaines [Université Paris-Sorbonne].
Titre et Sous-titres de cette première présentation de la méthode A.S.I. :
La naissance et/ou le diplôme. Analyse Structurelle des Interférences (A.S.I.) observables dans une table de mobilité sociale intergénérationnelle à trois dimensions. Essai de décomposition booléenne des relations numériques impliquées dans une structure complexe.
Il s’agissait du résultat d’un concours amical organisé par Philippe CIBOIS, qui proposait à différents volontaires (dont je faisais partie) le même tableau statistique à trois dimensions de répartitions numériques quantitatives sur le thème de la “mobilité socio-professionnelle intergénérationnelle” de manière à pouvoir comparer les résultats obtenus par différentes méthodes et leurs interprétations – comme ce fut déjà le cas pour un numéro précédent de la même revue (n° 32, mars 1977)
On peut regretter que cette revue (en tout cas à cette époque) n’était pas imprimée mais simplement ronéotypée couleur gris pâle (pratiquement mal reproductible sans les stencyls) – au format standard 21 x 29,7 cm. et brochée de manière très fragile, à manier avec précaution : le seul exemplaire que j’ai conservé étant disloqué. Mais on peut aussi regretter que les concurrents n’aient pas été associés à l’élaboration d’une ou plusieurs “problématiques” sociologiques, impliquant les identités socio-économiques de cet échantillon (représentatif ou non ?) de 3450 adultes travailleurs mâles (noter le sexisme peu surprenant de cette période) … ce qui nous réduits à ne “jouer le jeu” du concours que sur le plan thechno-statistique.
Ce tableau est un classique des recherches sur la mobilité intergénérationnelle en termes de catégories socio-professionnelles, que l’on doit au sociologique britannique David GLASS (1952) – dont nous n’avons pas eu pas à connaître ici la problématique habituelle en termes de division sociale du travail, de rapports sociaux de classes socio-économiques, de sexe (ou genre ?), de génération, de groupe ethnoculturel …. – tous critères nécessairement impliqués comme interférents avec l’origine familiale et le niveau d’études obtenu.
On trouvera plus loin les séries de nombres du codage de ces travailleurs dans leurs 3 répartitions, ainsi désignées :
i = Catégories socioprofessionnelles des enquêtés = de “type 1” [cadres sup. et prof. libér.], de “types 2 et 3 regroupés” [cadres moyens et subalternes], de “type 4” [ouvriers qualifiés et employés] et de “type 5” [ouvriers non qualifiés] ;
j = Formation scolaire des enquêtés = de “type 1” [dite “supérieure”], de “types 2 et 3 regroupés” [dite intermédiaire] et de “type 4” [dite “primaire”] ;
k = Catégories socioprofessionnelles de leurs pères = mêmes catégories que pour i = de “type 1” [cadres sup. et prof. libér.], de “types 2 et 3 regroupés” [cadres moyens et subalternes], de “type 4” [ouvriers qualifiés et employés] et de “type 5” [ouvriers non qualifiés] ;
On a colorié la catégorie i en rouge pour indiquer qu’elle a un statut très particulier dans cette enquête, car considérée comme la variable “dépendante”, postulée comme possiblement “sous l’influence” des deux autres “variables”. D’autre part, dans l’échelle du temps, j et k se positionnent dans l’antériorité de i – ce qui est bien conforme à une problématique de type causal. Et le paradigme du treillis distributif à 3 générateurs permet d’ analyser les effets de chacune des 2 variables “influentes” sur la 3ème – soit séparément “toutes choses égales par ailleurs” soit en exerçant leurs influences ensemble, en interférant plus ou moins l’une avec l’autre ….
Le problème des “effets” se complique si l’on admet le possibilité qu’ils se produisent (par ex. les attitudes, images, opinions, évaluations, à propos de tels métiers ou statuts d’emploi, par attraction et/ou par répulsion, ou avec indifférence, voire selon un processus mixte qu’on pourrait qualifier d’ “oxymorique” !
nb cases par critère = 1 cube et n carrés ——————–
A ma connaissance je fus le seul à avoir relevé ce défi méthodologique, ce qui n’a pas permis de comparer plusieurs méthodes différentes – mais ce qui m’a donné l’occasion d’exploiter de manière critique la méthode américaine dite de la “théorie de l’Information” (pratiquée en France par les psychologues Maurice FAVERGE et Françoise BACHER) en la nommant (avec l’approbation de Jacqueline FELDMAN, une collègue et amie à la fois mathématicienne et sociologue) “Analyse Structurelle des Interférences”. Mais la revue Informatique et Sciences humaines, dirigée par Marc Barbut, n’en a pas moins publié intégralement les 85 pages de cette analyse statistique novatrice en décembre 1978, sans autre commentaire qu’un échange avec Philippe Cibois qui me rappelait l’existence de la méthode “benzecriste” d’ “Analyse Factorielle” qui dominait alors les travaux de recherche sociologique en France.
Puis, suite à une présentation que je fis de cette méthode A.S.I. aux Journées annuelles de statistique de Toulouse en mai 1980 (ouvertes aux amateurs comme aux statisticiens professionnels), la revue de méthodologie de langue anglaise bien connue, Quality and Quantity, me proposa d’en publier une traduction anglaise – dont ma collègue et amie Paula Lew Faï, psychosociologue au Centre d’Ethnologie sociale et de Psycho-Sociologie du CNRS-EHESS, se chargea avec compétence. Et ce fut
Proposals for a Descriptive Analysis of Multidimensional Contingency Tables of unarrayed Numerical Distributions, in Quality and Quantity, N° 15-4, août 1981, pp. 365-401.
Cet article n’est pas accessible intégralement mais on peut accéder à ses deux premières pages imprimées (le “Review”) ainsi qu’à sa longue Bibliographie et à son contexte institutionnel, mais après s’être assuré que l’adresse de la présente “page” de mon Site Web – http://jacquesjenny.com/legs-sociologique/?page_id=380 – est bien inscrite sur la ligne de commande en Haut de votre écran, pour pouvoir y revenir par un clic avec la souris après cette consultation de Quality and Quantity …
… vous pouvez maintenant cliquer sur le lien du site éditorial de cette revue –>
https://link.springer.com/article/10.1007/BF00144061
Pour ma part, j’aurais souhaité que cette méthode A.S.I. fût aussi publiée dans la revue de sociologie plus “officielle” et moins “confidentielle”, à savoir la “Revue française de Sociologie” – dans laquelle était déjà publié en 1962 mon article thématique sur le processus de “maturation sociale” de l’enfance à l’âge dit adulte. Mais – comme je l’indique plus loin – les patrons et les mandarins de la recherche sociologique de cette époque en décidèrent autrement, lettre de refus à l’appui, sans même avoir fait l’effort de bien comprendre l’originalité et l’intérêt de cette méthode … dont j’ai la prétention de croire qu’elle pourrait accéder au statut de “révolution paradigmatique” avec son paradigme-clé de “treillis distributif à n générateurs – avec n=2 ou 3 voire 4 au maximum” … Au passage, je souhaiterais associer mon ancienne collègue et amie, ingénieure du CNRS (Françoise Tillion, soeur de Germaine, autre amie remarquable) qui m’a orienté sur la voie féconde de ce paradigme graphique que ne semblaient pas connaître les rares chercheurs pratiquant l’équivalent de ces mêmes formules logarithmiques, incomplet ou réduit à 2 générateurs
?
On pourra verra ci-dessous :
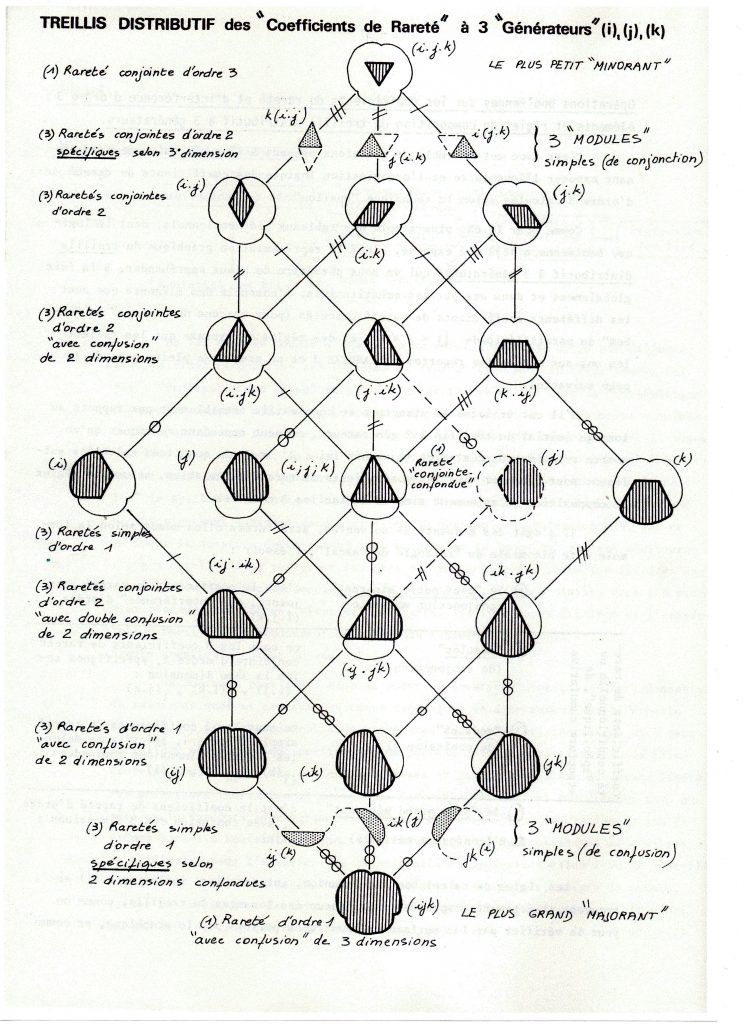
1 – la figure graphique booléenne de ce fameux “treillis distributif à 3 générateurs” que j’ai appliqué au tableau statistique à 3 dimensions de David GLASS comme nouvel Outil de la pensée au service d’une “révolution paradigmatique”, et qui justifierait à lui seul le mot de “legs sociologique” que j’ai souhaité donner à la partie “épistémologie et méthodologie et en sciences sociales” de mon site Web.
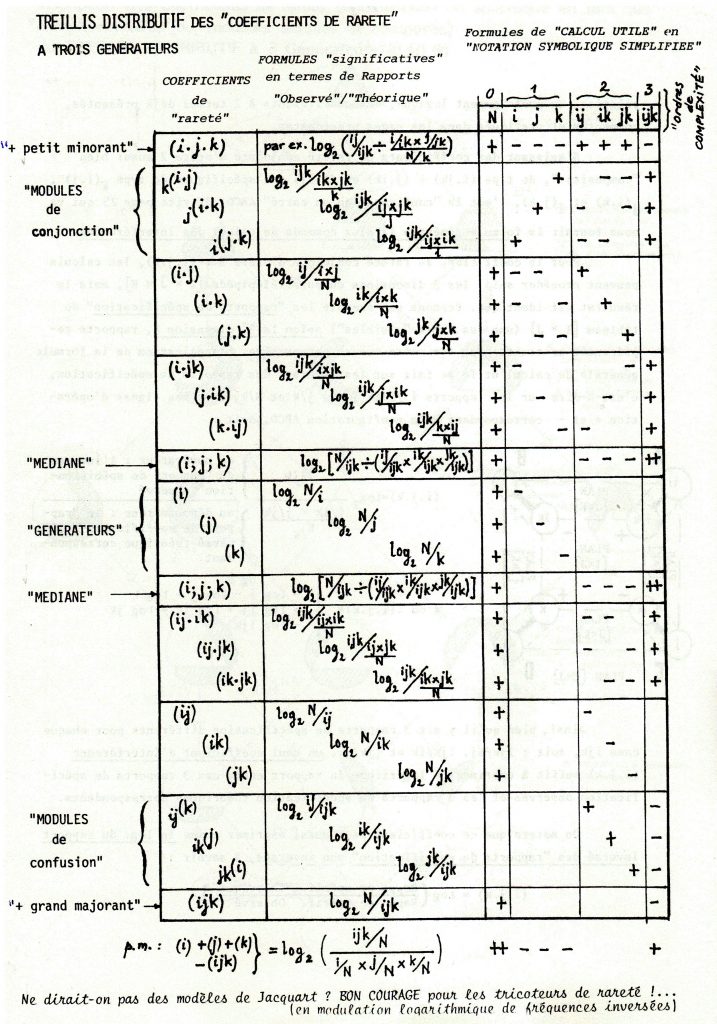
2 – puis, ci-dessous, le tableau des formules de calcul de toute la série des “coefficients de rareté” qui permettent de décrire la structure des Interférences qui se jouent entre les 3 catégories sociales décrivant cet “échantillon” de 3450 “individus… – à savoir :
i = C.S.P. [4 types] des enquêtés – tous masculins
j = “niveau scolaire” [3 types] des enquêtés
k = C.S.P. [4 types] de leurs pères
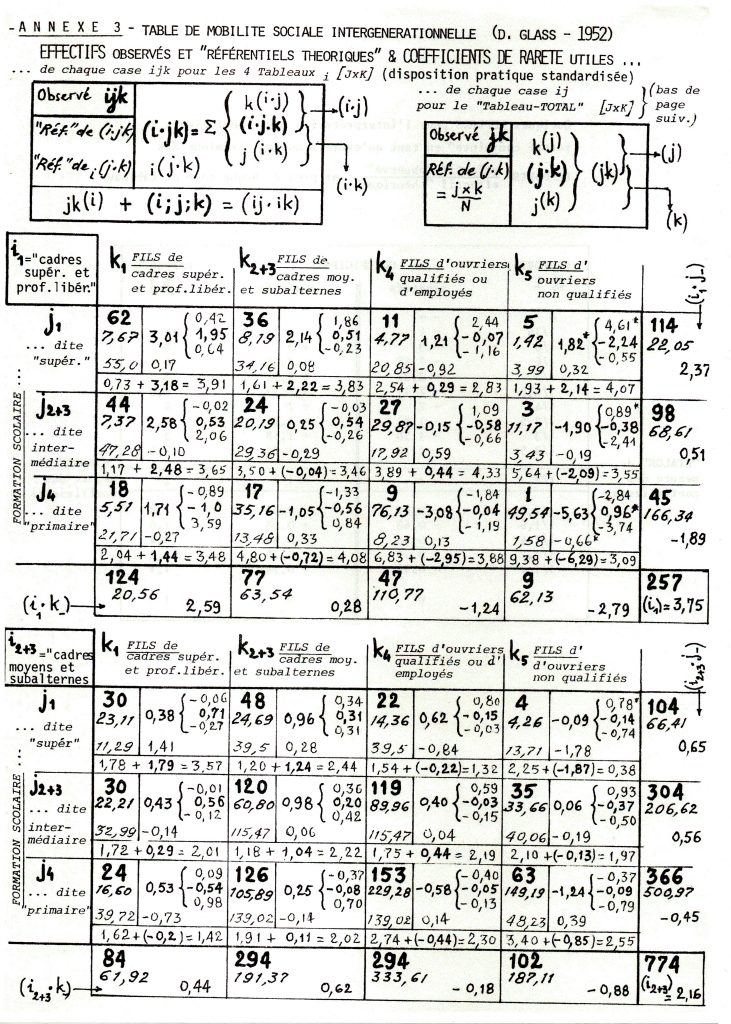
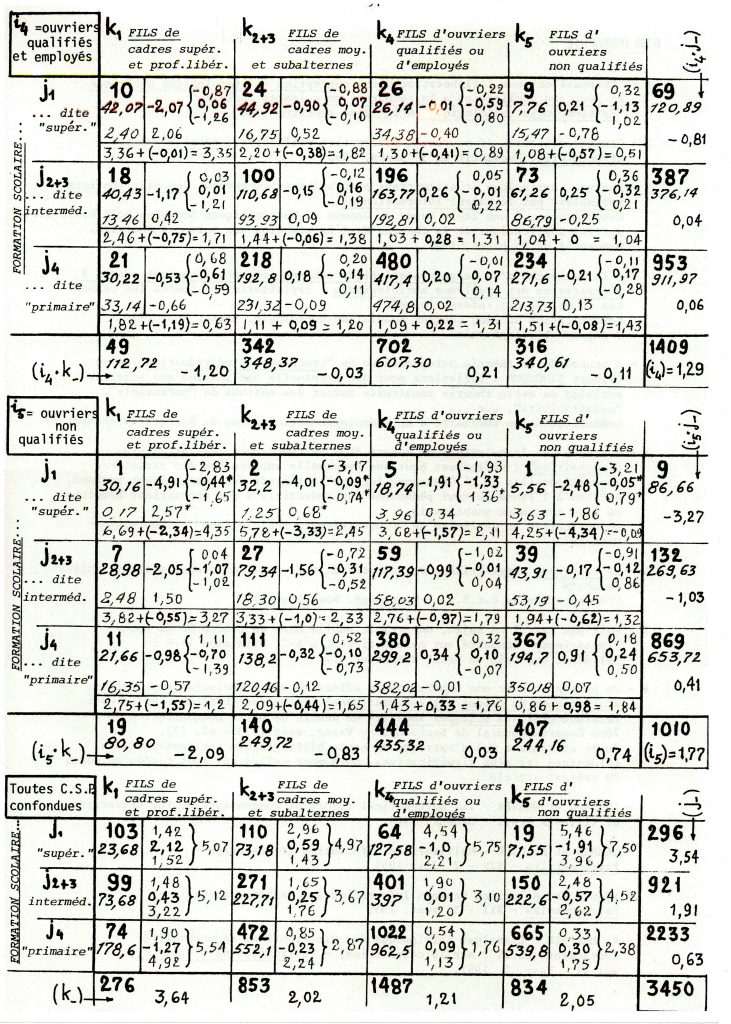
voir le tableau page suivante de la répartition tri-dimensionnelle de ces 3450 enquêtés HOMMES
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Je signale, avec toutes mes excuses, que cette “page” empirique de mon site Web est encore en chantier – notamment parce que les commentaires des variations de ces coefficients statistiques doivent recourir à des connaissances de type “qualitatif” (à rechercher dans les sciences sociales et dans les expériences humaines subjectives que tout citoyen britannique peut s’être faites au cours de la période de cette collecte des réponses …).
La “justification” de ce principe épistémologique est d’ailleurs exposée et développée dans la “page suivante” de mon site Web, intitulée :
“Quali / Quanti” = distinction fallacieuse et stérile !
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_______________________________________
La présente page de mon site Web retrace maintenant l’historique et le contexte théorique et épistémologique de cette bien nommée méthode A.S.I. (Analyse Structurelle des Interférences)
Dès le début des années 60 je me suis intéressé de près aux formules statistiques des psychologues américains Garner et Mac Gill, qui calculaient les variations de proportions des effectifs observés au sein de tables de contingence à 2 ou 3 dimensions en développant la formule bien connue (dite parfois de l’«entropie») de Shannon et Weaver [1]. L’ensemble structuré des formules de Garner et Mac Gill était d’emblée présenté comme l’équivalent logique des formules de décomposition de la variance de type Sigma pour des tableaux statistiques pluridimensionnels de type Upsilon et d’ordre de complexité 2 ou 3 – ce qu’on appelle couramment des tables de contingence multidimensionnelles. Mais la filiation de cette application statistique par rapport au paradigme de la communication et à la théorie de l’information, auxquels se référait Shannon, ingénieur de la Bell Telephone Company, fait qu’on en parle aussi parfois en termes de «calcul informationnel» : l’objectif y est en effet clairement désigné comme la recherche d’un moyen de mesurer des distributions (ici, transmissions de séries de sons, phonèmes ou messages) a priori non mesurables.
Après des tâtonnements empiriques de 1965 à 1970 et après un séjour fécond de deux années à l’Université de Montréal, j’ai eu l’intuition d’inscrire délibérément le formulaire de Garner et Mac Gill dans les structures complexes de l’algèbre de Boole (mieux pratiquées en France), notamment celle du «treillis distributif à n générateurs», apparemment moins connue outre-Atlantique [2] – ce qui m’a d’ailleurs amené à corriger une «erreur logique» dans ce formulaire. Et je décidai d’en faire une méthode à part entière, que j’appelai l’«Analyse Structurelle des Interférences» (= méthode A.S.I.) – convaincu que cette méthode originale et cohérente convenait parfaitement au traitement statistique des répartitions numériques complexes … Du moins de ces répartitions de groupements sociaux et catégories sociales auxquels m’ont accoutumé mes premières années de recherche, notamment dans les problématiques de “morphologie sociale”
La structure du treillis distributif à n générateurs exprime habituellement les effectifs dénombrés dans les différentes parties de la combinatoire (non arborescente) des réponses croisées à n Questions, dans les cases et dans les marges de tableaux multidimensionnels. Dans la méthode A.S.I., les effectifs sont remplacés par des coefficients de type Upsilon, et ces coefficients peuvent être ceux-là mêmes du calcul informationnel classique proposés par Garner et Mac Gill et repris tels quels par Faverge et Bacher (on les appellera alors coefficients d’«entropies de distribution» UPSILON) et/ou des coefficients propres à chacune des classes des n distributions croisées (on les appellera alors coefficients «de rareté» upsilon) [3]. Ces coefficients upsilon, dont les moyennes pondérées ne sont autres que les coefficients classiques UPSILON, me sont apparus dès 1965 comme plus conformes au type particulier de distributions non ordonnées (le «premier niveau» selon Stevens), si l’on veut analyser dans le détail toutes les variations proportionnelles observables dans des tableaux de contingence multidimensionnels. Certains de ces coefficients fournissent d’ailleurs une mesure des distances (ou écarts) entre les effectifs observés et les effectifs théoriques correspondants (calculés selon l’ «hypothèse nulle» d’absence de relations), avec possibilité d’en calculer des probabilités inférentielles.
Différentes formules de décomposition des effets confondus («réunion booléenne») en effets bruts ou superficiels, effets nets ou spécifiques, et effets conjoints ou interférences («intersection booléenne») permettent des analyses fouillées sur des batteries d’indicateurs exprimant des phénomènes ou des processus complexes. En général les problématiques de recherche sociologique suggèrent des «modèles d’analyse multivariée» sur lesquels l’analyse peut se concentrer, exactement comme on le fait en recherche expérimentale stricto sensu (par ex. en agronomie, depuis Fisher) et à peu près comme le fait la méthode dite «log-linéaire» qui est apparue quelques années plus tard, avec ses deux versions (backward et foreward).
L’objectif de la présente annexe n’est pas d’exposer en détail cette statistique Upsilon et cette méthode A.S.I., bien qu’elles mériteraient probablement d’être sorties du placard où certains mandarins les ont enfermées il y a plus de 20 ans en me refusant la publication d’un article dans la prestigieuse ( ?) Revue Française de Sociologie, mais aussi de là où la mode dominante des analyses de type spectral les a pratiquement mises à l’écart – comme c’est le cas en France avec le succès des A.F.C. (dont l’Analyse Factorielle des Correspondances à la Benzecri).
C’est pourquoi je n’en ai fourni ici que les principales caractéristiques, en renvoyant les lecteurs intéressés à deux articles (cités en introduction ci-dessus) concernant les présupposés, la conception et l’élaboration de ces outils et méthodes statistiques, avec une application commentée sur une table tridimensionnelle classique de mobilité sociale intergénérationnelle …
… notamment pour l’analyse des «effets d’interaction» (ou interférences) conçus comme constitutifs de la réalité sociale, et non comme épiphénomènes, …
Si l’on prend l’exemple empirique classique, voire emblématique, des processus de mobilité sociale intergénérationnelle (que ce soit dans leurs manifestations statistiques ou dans l’observation de cas cliniques ou de monographies comparatives), les effets d’interaction expriment comment et/ou combien une relation connue entre deux indicateurs (par ex. entre les positions sociales des parents et les positions sociales des enfants) varie, se transforme, lorsque l’on spécifie un troisième indicateur (par ex. le sexe et/ou le cursus scolaire des enfants), et ainsi de suite lorsque l’on passe de l’ordre de complexité 3 à 4, puis de 4 à 5, etc ….
Il s’agit en somme de concevoir une méthodologie conforme au principe suivant de “complexité optimum“, qui appellerait évidemment de longs commentaires épistémologiques et théoriques par rapport au Discours Cartésien de la Méthode :
“construire, enregistrer et traiter les informations
sous la forme (dans le ‘format’) la plus signifiante pour la recherche,
c’est-à-dire à leur ‘niveau de complexité’ le plus élevé possible“.
Ce postulat de la complexité implique que les effets d’interaction (appelés parfois aussi effets multiplicatifs par opposition à de simples effets additifs), que je préfère appeler interférences, sont constitutifs au moins potentiellement de toute réalité sociale et humaine – et ne sont ni de simples épiphénomènes ou artefacts ni des brouillages aléatoires de relations simples et stables. En outre, ces interférences sont éminemment heuristiques en ce qu’elles peuvent contredire, ou nuancer fortement, des liens déjà imprudemment établis en lois générales : leur évaluation ne devrait donc pas être une option facultative, mais être la règle, partie intégrante de tout programme d’analyse minimum, comme nous l’enseignaient Lazarsfeld et Boudon en termes de “corrélations fallacieuses”. L’absence éventuelle d’interférence serait alors à considérer comme une exception à la règle, résultat tout aussi remarquable.
C’est une raison supplémentaire de mes réserves à l’égard des méthodes d’analyse de type spectral, qui réduisent la complexité pluridimensionnelle en une véritable analyse au sens de décomposition par juxtaposition additive de «facteurs explicatifs» unidimensionnels, là où l’on postule pourtant que la structure complexe est de type booléen.
Certes une telle structure est plus difficile à synthétiser que les illusoires syncrétismes des analyses spectrales, mais cette conception «multiplicative» de la complexité peut nous engager dans des constructions théoriques et paradigmatiques beaucoup plus fécondes et heuristiques que certains paradigmes dominants d’un déterminisme sociologique d’apparence multiforme (par ex. les différents registres interdépendants de «capital», dans la sociologie de Bourdieu) mais au fond assez simpliste.
… et la mise en œuvre pratique de cette méthode grâce aux procédures interactives et conviviales des nouveaux outils micro-informatiques
Pour faciliter le calcul des formules de cette méthode A.S.I., qui fait appel à la transformation logarithmique, j’ai dû programmer moi-même, en autodidacte, les programmes informatiques nécessaires – d’abord sur des calculettes programmables dès qu’elles apparurent sur le marché [4], puis en langage Basic sur les premiers micro-ordinateurs de bureau dans le cadre d’un logiciel plus général d’analyse d’enquêtes sociologiques que j’ai développé à partir du logiciel SADE de l’Université de Franche-Comté.
Si j’ai choisi ce logiciel SADE (= Saisie Assistée et Dépouillement d’Enquêtes) c’est parce qu’il m’était apparu à l’époque comme le plus conforme à mes conceptions méthodologiques du traitement de la complexité de l’information sociologique, notamment en ce qu’il prévoyait (ce qui était rare à l’époque) de mélanger des questions de tout format, de la question précodée simple classique aux questions ouvertes appelant des réponses en langage naturel. Et j’y ai progressivement introduit une typologie bidimensionnelle du «format» des questions, destinées surtout à enregistrer et traiter des questionnements composites ou complexes comme ceux que les sociologues utilisent spontanément ou pourraient utiliser, avec un peu d’imagination : s’ajoutant aux questions simples à réponse unique, on y trouve les «batteries de questions» et les questions-tableaux, les questions «plurielles» et les questions «structurelles ou contextuelles» (pour informations concernant des groupes ou des réseaux). Le tout étant combiné avec les trois principaux «niveaux de mesure» classiquement distingués et le langage naturel (en réservant pour le futur proche un type appelé «multimedia» comme y invitent les NTIC, Nouvelles Technologies de l’Information et de la Communication), cela représente en tout 5 fois 5 = 25 formats différents de questionnements :
| “dispositif de | types | de | réponse | sollicitée | |
| questionnement“ | |||||
| Nombres | Rangs | Codes | Texte | “multimedia” (p.m.) | |
| QRU = 1 Q / 1 R | A | B | C | D | E~ |
| QRM = 1 Q / x R | F | G | H | I | J~ |
| nQRU = n Q / 1 R | K² | L² | M | N | O~ |
| nQRM = n Q / x R | P~ | Q~ | R~ | S~ | T~ |
| QTAB = m l * n c | U~ | V~ | W~ | X~ | Y~ |
[Q= Question / R= Réponse] [l= ligne / c= colonne]
RU= Réponse Unique RM= Réponses Multiples QTAB= Quest.-Tableau
nombres : m & n = déterminés x = indéterminés
exposants : ² = en cours de développement logiciel ~ = extension logicielle en projet
___________________________________________
Mes conceptions méthodologiques impliquent également la nécessité de développer des procédures à la fois plus conviviales et mieux adaptées à la spécificité des sciences sociales que les principales méthodes décrites dans les manuels ou implémentées dans les logiciels usuels d’analyse d’enquêtes, de type généraliste. A cet effet j’ai particulièrement soigné l’«ergonomie cognitive» pour l’impression/affichage des résultats de tri et de calcul, notamment en pratiquant des formats d’impression le plus condensés possible pour faciliter la lecture synoptique des grands tableaux, voire de «tableaux de tableaux conditionnels», fort appréciés des utilisateurs.
Dans le même esprit, j’ai programmé des modules de «relecture» des classifications arborescentes (par permutation de l’ordre d’affichage des combinaisons de réponses triées, l’équivalent de ce qu’on appelle maintenant «arbres de décision») très conviviales, pour inciter les chercheurs à multiplier sans effort particulier autant de lectures de structures complexes que leur curiosité peut leur en suggérer.
D’ailleurs ma maquette de logiciel a déjà servi pour quelques grandes enquêtes psychologiques ou psychosociologiques et pour de nombreuses enquêtes sociologiques. Certaines de ces enquêtes ont abouti à des publications remarquées et/ou ont porté sur des populations étrangères ou sur des comparaisons internationales ; quelques dizaines de thèses de doctorat en sociologie ont utilisé ce logiciel, avec profit selon leurs auteurs.
Comme j’ai accompagné de près la plupart de ces applications, des plus modestes aux plus prestigieuses, et que je suis constamment resté à l’écoute des chercheurs, ce logiciel a beaucoup profité de la diversité des problèmes rencontrés – à l’intersection de la méthode et de la théorie – et s’est enrichi de plusieurs fonctionnalités. Un examen récent des plus importants des logiciels comparables actuels m’a confirmé que certaines de ces fonctionnalités ne figurent dans aucun de leurs cahiers des charges, et que certaines des conceptions à l’œuvre dans mon logiciel sont (encore) originales par rapport aux présupposés et postulats implicites de cette catégorie de logiciels.
C’est pourquoi je lance ici un appel désintéressé mais pressant aux concepteurs de logiciels actuels et potentiels en espérant qu’il se trouvera parmi eux un repreneur de ce projet, projet bien avancé mais maintenant en friche : je mets à leur disposition, sans aucune contrepartie financière, tous les éléments de ce dossier – y compris évidemment les programmes-sources de tous les modules qui composent ce logiciel.
[1] la paternité états-unienne de cette méthode est usurpée dans la mesure où on peut lui trouver des antécédents méconnus, en la personne du japonais Watanabé et de notre compatriote Etienne Halphen, statisticien méconnu pour lequel j’ai une très grande estime. Mais peu importe, pour l’objet qui nous occupe ici et maintenant ….
[2] Ajoutons pour la petite histoire que c’est hors de ma «communauté» des sociologues francophones que j’ai été reconnu comme co-inventeur de la formule exacte du «point médian du treillis distributif à 3 générateurs». Comme quoi l’ «ingénuité intellectuelle» peut s’avérer payante en matière de création, mais aussi comme quoi la bureaucratie du CNRS associée au mandarinat de l’Université peut parvenir à étouffer des propositions originales, en ne permettant même pas qu’elles soient mises à l’épreuve et a fortiori en refusant le soutien logistique et humain nécessaires pour leur développement.
[3] Une des originalités de la méthode A.S.I. est en effet de compléter les formulaires d’entropies de distribution du calcul informationnel classique par autant de formulaires qu’il y a de cases dans un tableau multidimensionnel, selon la formule log.1/p induite de la somme pondérée calculée sur toutes les classes de chaque distribution, à savoir Somme (p log.1/p) – où les p sont les proportions des effectifs de chaque classe.
[4] sur cet aspect technique précis, on pourra consulter le site Web personnel d’un collègue ethnologue, Noël Jouenne, qui y présente un historique des usages des calculatrices électroniques de poche depuis 1972, en y ajoutant la description d’un prototype de «règle à calcul informationnel» que j’avais conçu et réalisé dès 1965, avant l’apparition de la fonction log. sur ces calculettes : http://perso.wanadoo.fr/noel.jouenne/index.html